Füllgewichte von Kakaopackungen

Berechnen Sie die Wahrscheinlichkeit dafür, dass das Füllgewicht einer beliebigen Packung

• zwischen $124{,}5 \,\text{g}$ und $125{,}4 \,\text{g}$ liegt,
• über $127{,}0 \,\text{g}$ liegt,
• höchstens $122{,}0 \,\text{g}$ oder mindestens $128{,}0 \,\text{g}$ beträgt.

Bestimmen Sie das größte Gewicht, das mindestens $95 \,\%$ der Packungen überschreiten.

1. Zwischen $124{,}5 \,\text{g}$ und $125{,}4 \,\text{g}$

Wahrscheinlichkeit als Intervall formulieren

Gesucht ist

$$P(124{,}5 \le X \le 125{,}4).$$

Die Normalverteilung ist durch

$$\mu = 125, \qquad \sigma = 2$$

gegeben.

Mit CAS berechnen

Taschenrechnerbefehl

1. $\boxed{\text{menu}}$
2. Wahrscheinlichkeit (5)
3. Verteilung (5)
4. Normal Cdf (2)

$\boxed{normCdf(124.5,125.4,125,2) \approx 0.178}$

Antwort

Die Wahrscheinlichkeit, dass das Füllgewicht zwischen $124{,}5 \,\text{g}$ und $125{,}4 \,\text{g}$ liegt, beträgt ungefähr $17{,}8 \,\%$.

Der Hersteller überprüft seine Abfüllmaschine. Dafür untersucht er $500$ Packungen, die von dieser Maschine abgefüllt wurden. Ein zu geringes Füllgewicht ist gegeben, wenn dieses mehr als $4{,}5 \,\text{g}$ unter dem Erwartungswert liegt.

Zeigen Sie die Gültigkeit der folgenden Aussage mithilfe einer geeigneten Binomialverteilung:

„Die Wahrscheinlichkeit dafür, dass mehr als $2 \,\%$ der Packungen ein zu geringes Füllgewicht haben, beträgt etwa $4{,}6 \,\%$.“

Ein Großhändler erhält $10$ Lieferungen mit jeweils $500$ Packungen. Berechnen Sie die Wahrscheinlichkeit dafür, dass bei höchstens einer dieser Lieferungen mehr als $2 \,\%$ der Packungen ein zu geringes Füllgewicht haben.

Gültigkeit der Aussage

Höchstens eine Lieferung

Einzelwahrscheinlichkeit bestimmen

„Zu geringes Füllgewicht“ heißt:

$$X < 125 - 4{,}5 = 120{,}5 \,\text{g}.$$

Gesucht ist also

$$p = P(X < 120{,}5).$$

Die Normalverteilung ist durch

$$\mu = 125, \qquad \sigma = 2$$

gegeben.

Einzelwahrscheinlichkeit mit CAS berechnen

Taschenrechnerbefehl – Normal Cdf

1. $\boxed{\text{menu}}$
2. Wahrscheinlichkeit $(5)$
3. Verteilung $(5)$
4. Normal Cdf $(2)$

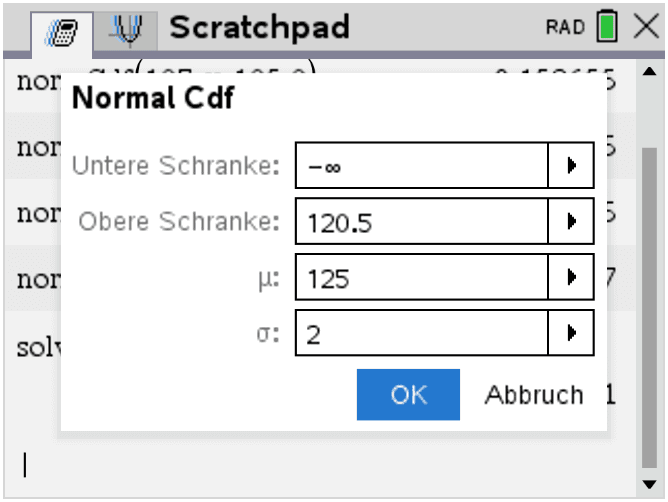
$\boxed{\text{normCdf}(-\infty,120.5,125,2) \approx 0.012}$

Also:

$$p \approx 0{,}012 \quad\Rightarrow\quad 1{,}2 \,\% \text{ zu geringe Packungen}.$$

Binomialverteilung ansetzen

Es werden $500$ Packungen untersucht. Zufallsvariable:

$$Y = \text{„Anzahl der Packungen mit zu geringem Füllgewicht“}.$$

Damit:

$$Y \sim \text{Binomial}(n = 500, p \approx 0{,}012).$$

„Mehr als $2 \,\%$“ von $500$ Packungen bedeutet:

$$0{,}02 \cdot 500 = 10.$$

Gesucht ist also:

$$P(Y > 10) = P(Y \ge 11).$$

Binomialwahrscheinlichkeit mit CAS berechnen

Wir verwenden die kumulierte Verteilung $P(Y \le k)$.

$$P(Y \ge 11) = 1 - P(Y \le 10).$$

Taschenrechnerbefehl – Binomial Cdf

1. $\boxed{\text{menu}}$
2. Wahrscheinlichkeit $(5)$
3. Verteilung $(5)$
4. Binomial Cdf $(B)$

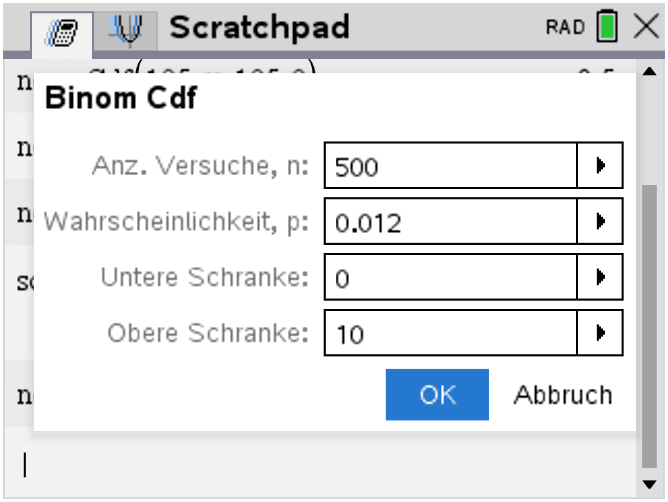
$\boxed{\text{binomCdf}(500,0.012,0,10) \approx 0.958}$

Also:

$$P(Y \ge 11) = 1 - 0{,}958 \approx 0{,}046$$

Antwort

Die Wahrscheinlichkeit, dass bei $500$ Packungen mehr als $2 \,\%$ ein zu geringes Füllgewicht haben, beträgt ungefähr

$$4{,}6 \,\%.$$

Die angegebene Aussage ist damit zutreffend.

Unabhängig vom Sachzusammenhang ist die normalverteilte Zufallsgröße $X$ mit dem Erwartungswert $\mu = 125$ und der Standardabweichung $\sigma = 2$ gegeben.

Betrachtet werden Intervalle $[a;b]$ mit folgenden Eigenschaften:

• $a$ und $b$ sind beide größer als der Erwartungswert.
• Der Abstand vom Erwartungswert ist für $b$ doppelt so groß wie für $a$.

Bestimmen Sie die beiden Werte von $a$, für die gilt: $P(a \le X \le b) = 0{,}1$.